230201 1L2L0X0C_(I), http://farbe.li.tu-berlin.de/CEJI.HTM or
http://color.li.tu-berlin.de/CEJI.HTM
For this main page with general information and special images
of the corresponding image page with 10 colour series, see
CEJI in English,
CGJI in German.
For the previous main page, see
CEII in English,
CGII in German.
For the next main page, see
CEKI in English,
CGKI in German.
For links to the chapter C
Colour Spaces, Colour Differences, and Line Elements (2021),
see
Content list of chapter C:
CEA_I in English or
CGA_I in German.
Summary of chapter C:
CEA_S in English or
CGA_S in German.
Example image part of 26 parts CEAS to CEZS:
CEAS in English or
CGAS in German.
Chapter C: Colour Spaces, Colour Differences, and Line Elements (2021),
Main part CEJI
1. Introduction and Goals
The coordinates of colour spaces and of the colour differences
are connected by line elements. For example Schroedinger (1925)
and Stiles (1946) have tried to develop line elements for this
connection.
Schroedinger, E. (1925), The relationship of
Four-Colour Theory and Three-Colour Theory, Sitzungsberichte
Kaiserl. Akad. Wiss., Wien, [IIa] 134, 471-490.
Stiles, W. S (1946), The line element in colour theory:
a historical review, p. 1-25, in Color metrics, AIC/Holland,
TNO Soesterberg.
A special case of a colour difference is the threshold colour
difference. At threshold the colour difference of two adjacent
colours are recognized with a probability of 50%. Usually after adaptaion
and fixation of the two adjacent colours the observer detects a
difference for 50% of the viewing time and detects NO difference
for 50% of the viewing time.
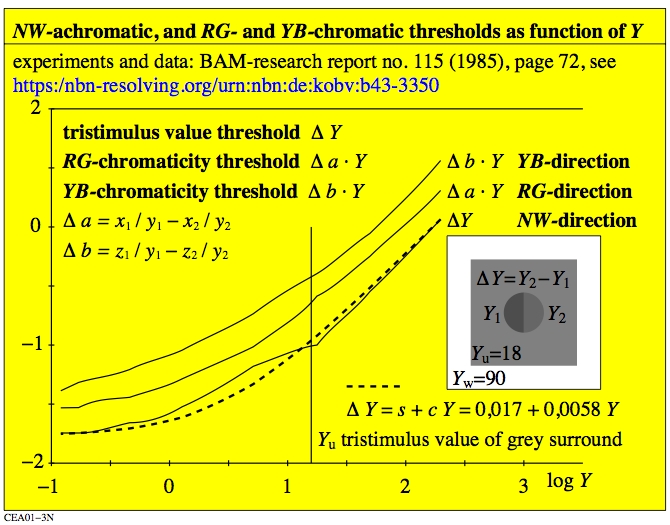
Figure 1: Visual threhold delta_Y of achromatic and chromatic
samples in a grey surround with a white frame.
For the download of this figure in the VG-PDF format, see
CEA01-3N.PDF.
The figure shows that the threshold delta_Y
increases approximately linear with Y with the slope 0,86.
This slope is near the value 1. In this case the so called
Weber-Fechner ratio Y/delta_Y
is approximately constant within the range 10 <= Y <= 100.
For the very smal tristimulus values Y < 0,4
it is valid delta_Y=0,012.In applications for all
values Y < 0,4 the two central field colours appear
as a uniform deep black.
The results in Fig. 1 are the basis of the colour-difference formula
LABJND for Just Noticeable Differences (JNDs) in CIE 230:2019.
The performance of LABJND_PF is calculated in Table 9 and 11 of CIE 230
for the scope range 0 <= delta_E*ab <=2
of the CIELAB colour-difference formula,
and for the 8 available CIE datasets, see
http://files.cie.co.at/TC181_Datasets.zip.
The extension "_PF" describes a modification of the LABJND-colour difference
which produces the value (delta E*)LABJND = 1 at threshold. A "power
function correction PF", for example with an exponent n=0,5,
does not change the colour difference. However, for 100 threshold
differences for example an exponent n=0,5 reduces the colour
difference from the value 100 to the value 10:
(delta E*)LABJND_PF = 100^0,5 = 10
A paper of Richter (2006) includes a model with an explanation,
see A/BAMAT.PDF. According to
this paper the local effective relative luminance (Leff)
of two adjacent greys is given by the equation:
log(Leff) = 0,5 [log(L1)+log(L2)]
If for example the relative luminance L1 is equal to the
relative surround luminance Lu=1 and L2=100Lu,
then it is valid:
log(Leff) = 0,5 [log(Lu)+log(100Lu)]
= 0,5 [0 + 2] = 1 = log(10)
The visual effective relative luminance at the border
of the two samples is Leff=10 and NOT L2=100.
This produces half of the slope with a value n=0,5
instead of 1. For the threshold the calculated colour
difference is equal for the values n=1 and 0,5.
In CIE 230:2019 the PF-value n was optimized for the
following five colour difference formulae:
CIELAB_PF (n=0,55),
CMC_PF (n=0,66),
CIE94 (n=0,70),
CIEDE2000_PF (n=0,70), and
LABJND_PF (n=0,35).
The PF-value n (in brackets) is the smallest for the
LABJND-threshold formula with the smallest colour-difference unit.
Eight datasets for small colour differences were studied and used
in CIE TC1-81. TC1-81 has produced the publication CIE 230.
The LABJND_PF colour difference formula shows the best performance for
5 out of 8 CIE datasets. CIELAB_PF, CMC_PF, and CIEDE2000_PF
show the best performance for one out of 8 CIE datasets.
In 2016 CIE TC1-63 has produced in WD11 results for large colour differences.
The comparison of the five formulae for Large (LCD) and Extra Large (ELCD)
colour differences shows about the same performance for all formulae, see
YE370-7N.PDF.
However, for Extra Large Colour Differences (ELCD)
with ratio and interval scaling the performance is different, see
YE330-7N.PDF.
The performance of LABJND_PF is better than for all other formulae.
The STRESS value according to CIE 217 is reduced from about 35 to 40
of the four above formulae to about 25 for LABJND_PF. Smaller
values describe a better performance.
According to the terms of reference for CIE TC1-63
the results shall be compared for the scope range
5 < delta_E*ab < 199.
In 2016 the CIE TC1-63 members could not agree to proceed
with the draft WD11 for a CIE Technical Report on Large (LCD)
and Extra Large (ELCD) colour differences.
The unexpected and conflicting result compared to the above
recommended CIE colour difference formulae may be a reason.
The results of
1. in WD11 of CIE TC1-63 and
2. on this web site
seem to be a promising basis for improved results in the area of:
Colour Spaces, Colour Differences, and Line Elements.
For more information about "line elements" and "metrics", see
DEAI.HTM.
-------
For the archive information (2000-2009) of the BAM server "www.ps.bam.de"
(2000-2018)
about colour test charts, colorimetric calculations,
standards, and publications, see
indexAE.html in English,
indexAG.html in German.
Back to the main page of this TUB web site (NOT archive), see
index.html in English,
indexDE.html in German.
